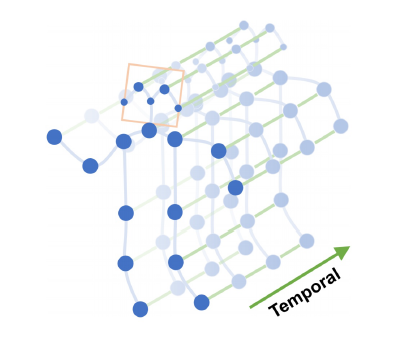
Spatial Temporal Graph Convoutional Networks (ST-GCN)
1. 논문 소개 및 주제
- 제목 : Spatial Temporal Graph Convolutional Networks for Skeleton-Based Action Recognition
- 저자 : Sijie Yan, Yuanjun Xiong, Dahua Lin
- 학회 : Thirty-second AAAI conference on artificial intelligence
발표 년도 : 2018
- 사람 골격데이터를 기반으로한 행동인식 연구
- Graph Convolutional Networks(GCN) 의 변형으로 시공간 그래프를 학습시키는 ST-GCN 소개
Kinetics, NTU-RGB+D 데이터셋으로 실험
- 구현 코드 깃허브 https://github.com/yysijie/st-gcn
2. 연구 동기
- 기존 hand-craft parts or traversal rules based 연구들에서 나타나는 아래 문제점 해결을 위해
1) 골격 표현의 종속성 : 데이터베이스에서 제공하는 관절 개수, 표현 방식에 종속됨
2) 데이터베이스 특화된 실험결과로 인한 일반화의 어려움
3. 주요 공헌점
1) ST-GCN 설계 : 골격 데이터 기반 행동인식 연구에 최초로 GCN 응용
- 입력으로 주어지는 관절을 자동적으로 시공간적 관계 연결하므로 기존 연구들과 같이 골격을 손수 만들어 입력으로 주어질 필요가 없어 행동을 표현하는 모델을 만들기가 쉬워진다.
- 관절마다 학습가능한 시공간 연결선(엣지)를 가진다.
- spatial edge : 한 프레임 상 관절들의 관계를 표현
- temporal edge : 연속된 프레임들 상에서 한 관절에 대한 시간축 연결을 표현
2) 골격 데이터에 맞게 디자인된 ST-GCN convolution kernel 설계
3) 대용량 데이터셋인 NTU-RGB+D / Kinetics 데이터셋에서 기존 연구보다 적은 노력으로 우수한 성과를 얻음
4. 제안 모델
1) 입출력
- 입력 : 관절 좌표 벡터가 각각 그래프의 노드에 입력
- 출력 : 특징벡터로 추상화된 골격데이터를 softmax를 거쳐 행동 카테고리로 분류
2) Skeleton Graph Construction
비방향성 그래프 : $G = (V, E)$
노드 집합 : \(V = {v_{ti} | 1 <= t <= T, 1 <= i <= N}\)
각 노드에 입력된 특징 벡터 : $F(v_{ti})$
두 종류 엣지 집합 :
- intra-skeleton edge : 인체에서 자연스럽게 연결된 관절 집합 (= spatial edge)
- inter-frame edge : 한 관절에 대한 trajectory over time (= temporal edge)
3) Skeleton Graph Convolution Neural Networks
특정 &\tau& 시각, 한 프레임 내에서의 그래프 컨볼루션 네트워크를 먼저 설계한다. 그래프 내에는 N개의 관절이 있고, 각 노드들은 위에서 제시된 집합에 속한다. 하지만 엣지는 spatial edge만 설계하므로
| $E_{S}(v_{ti}) = {v_{ti},v_{tj} | t = \tau, (i, j) \in H}$ |
집합에 속하게 된다.
그래프에서 컨볼루션 연산은 기존 CNN에서 컨볼루션 연산이 입력으로 주어진 2D 이미지나, 특징맵과 출력으로 나오는 특징맵을 2D 그리드 처럼 다룬것과 비슷하다. 먼저, 기존 KxK 컨볼루션 연산이 stride = 1, 적절한 padding으로 c개 채널을 가지는 입력 특징맵과 출력 특징맵의 사이즈가 같게 한다고 가정하자. 이때, 한 채널상의 x 위치 연산 결과는 아래와 같다.
\[f_{out}(x) = \sum^{K}_{h=1}\sum^{K}_{w=1} f_{in}(p(x, h, w)) \cdot \mathrm{w}(h, w)\]위 식에 주목해야 할 점은 sampling function, p와 weight function, w이다.
(1) sampling function, p : $\mathbb{Z}^{2} \times \mathbb{Z}^{2} -> \mathbb{Z}^{2}$
- 입력으로 주어지는 2x2 특징맵에서 특징을 추출할 x 근처 이웃들을 샘플링한다.
- 따라서 다음과 같이 표현할 수 있다.
(2) weight function w : $\mathbb{Z}^{2} -> \mathbb{R}^{c}$
- 각각 c개 채널을 가지는 샘플링된 입력과 가중치 벡터가 내적을 통해 c개 원소를 가지는 벡터가 된다.
4) Spatial Temporal Modeling
(1) the sampling function
이미지에서 이웃 픽셀들은 x를 중심으로 컨볼루션 필터 크기만큼 거리를 가지게 동서남북으로 모여있었다. 반면, 그래프에서는 각 노드들 마다 가지는 이웃노드가 다르기 때문에 이를 샘플링해 줄 수 있는 새로운 샘플링 함수가 필요하다. 이웃노드 집합을
\[B(v_{ti}) = {v_{ti} | d(v_{ti}, v_{tj}) <= D}\](d : the minimum length of any path from $v_{ti}, v_{tj}$)
라고 정의하면, 그래프에서 샘플링 함수 p는 다음과 같다.
\[the sampling function p : B(v_{ti}) -> V\] \[p(v_{ti}, v_{tj}) = v_{tj}\](2) the weight function
가중치 맵은 특징이 되는 곳을 짚기 위한 것이라 이미지에서는 중앙을 강조했다. 하지만, 그래프에서는 이렇게 한 곳을 특정할 수 없으므로 Niepart 논문에서 제안한 Graph Labeling Process를 따른다. 본 논문에서는 이를 골격데이터에 맞게 간단하게 정의하고자 이웃 노드 집합을 특정 K개의 고정된 하위집합으로 나누어 번호를 매긴다. 이 번호가 현재 노드에서 이웃하는 노드가 속하는 부분의 라벨이 되는 것이다. 쉽게 말하자면, 각 현재 선택된 관절에서 이웃이 되는 관절들이 속할 수 있는 부위를 하위집합으로 나타내고 이에 각기 다른 번호를 매기는 방식이다. 이를 수식으로 정의하면 다음과 같다.
mapping \(l_{ti} : B(v_{ti}) -> {0, ..., K-1}\)
\[w(v_{ti}, v_{tj}) : B(v_{ti}) -> \mathbb{R}^{c}\] \[w(v_{ti}, v_{tj}) = w`(l_{ti}(v_{tj}))\]정리하자면, 본 논문에서 정의되는 그래프 컨볼루션은 이웃노드들의 집합에 내적 연산을 하는 것이다. 여기서 이웃노드들 집합은 각각 라벨로 표현되며, 이 라벨을 정하는 규칙은 다음 절에서 소개한다.
5) spatial temporal modeling
앞서 한 프레임 내에서 각 관절을 모델링 한 것에 더하여 시간축으로 각 관절을 다음 프레임에서의 위치에 연결해줄 것이다. 먼저, 한 관절 $v_{ti}$ 의 시간축 이웃노드 집합은 아래 수식으로 정의된다.
\[B(v_{ti}) = {v_{qj} | d(v_{tj}, v{ti}) <= K, |q-t| <= \lfloor{\Gamma / 2}\lfloor \times K}\]위 식에서 $\Gamma$는 시간 범위를 조정하는 상수이고, temporal kernel size라 부른다. 이를 풀어서 말하자면, q 시각에서 이전 t 시각에 i와 K만큼 떨어져 있었던 j번째 관절들의 집합이 B이다. 여기서 $\Gamma$가 2로 나눠지고 있는 것은 B가 한 프레임에서만 정의되므로 t를 중심으로 q만큼 이전이거나 다음이거나 둘중 하나의 경우만 선택하니 2로 나눠진 시간 범위를 사용한다.
이를 이용하여 시간축 이웃노드 집합 라벨을 붙여줄 차례인데 이전 공간축에서와는 다르게 샘플링 함수와 가중치 함수를 정의하지 않는다. 그 이유는 공간축에서는 각 노드에서 컨볼루션 연산시에 필요한 이웃노드가 그래프에서는 이미지와 달라 따로 정의하였지만, 시간축은 이미 정리된 순서로 입력되고 있고 각 노드들은 그 순서에 맞춰 이웃을 가지기 때문에 부가적으로 정의가 필요치 않다. 따라서, 이웃노드 집합 정의에 따른 라벨링 수식은 아래와 같다.
\[l_{ST}(v_{qj}) = l_{ti}(v_{tj}) + (q - t + \lfloor{\Gamma / 2}\lfloor) \times K\]