[네이버 부스트캠프 AI Tech 6기] 최대 가능도 추정 (Maximum Likelihood Estimation, MLE)

1. 가능도(우도) 함수 (Likelihood)

• 파라미터(모수)를 가지는 모델을 추정할 때 가장 쉽게 고려할 수 있는 방법이 최대 가능도 추정법이다. 여기서 말하는 가능도는 추정하는 파라미터가 현재 관측된 데이터들을 얼마나 적합하게 설명하는지 알아볼 수 있는 측도이다. 이는 확률로 표현되는 것 같지만 확률과는 엄연히 다르다. 그 이유는 아래와 같다.

1) 확률과 우도의 차이

(1) 확률 vs 우도

• 확률은 주어진 파라미터에 대해 특정 데이터가 발생할 확률을 말한다. 확률은 주어진 데이터가 이미 발생했을 때 계산할 수 있다.
• 반면 우도는 주어진 데이터를 기반으로 “파라미터 값에서 주어진 데이터가 얼마나 가능한지” 를 측정하는 것이다.

(2) 계산 불가능성

• 가능도 함수를 계산할 때, 주어진 데이터는 이미 발생했다는 가정 하에 추정하는 각 모수에 대한 가능도를 계산한다. 이때, 현실적으로 모든 가능하는 파라미터에 대해 우도를 정확하게 계산하는 것은 불가능하다. 즉, 우도는 추정하는 모든 파라미터에 대해 구해서 다 더해도 1이 될 수 없다. (예를 들어, 정규분포에서 평균을 추정하면 가능한 범위는 정규분포가 정의되는 모든 실수가 될 것이다.)
• 따라서, 확률밀도함수에서 확률을 직접적으로 확률 계산이 불가능 하므로 우도를 사용하게 된다.
  

따라서, 가능도 함수는 확률이 아니다. 그럼 가능도는 어떻게 정의되는 것일까?

2) 가능도함수(우도, Likelihood)

• 먼저 주어진 데이터에 대한 확률분포 \(X\)에 대한 확률밀도함수 또는 확률질량함수는 아래와 같이 정의한다.

\[p(x;\theta)\]

• 여기서 \(x\)는 확률분포가 가지는 데이터이며 실수값이다. \(x\)는 n차원으로 표현될 수 있고, \(\theta\) 는 확률밀도함수의 파라미터(모수)를 뜻한다.

• 만약 확률분포가 정규분포나 이항분포이면 아래와 같이 표현된다.

정규분포 : \(\theta = (\mu, \sigma^2)\)
이항분포 : \(\theta = (N, \mu)\)

• 일반적으로 우리는 데이터를 수집할 뿐, 그 데이터가 어떤 분포를 가지고 있어서 추출되었는지 알 수 없다. 따라서 데이터에 대한 예측이나 군집화 등을 진행할때 데이터를 표현할 수 있는 적절한 모델을 선택해야 한다.
• 이때, 우리가 추측한 모델이 현재 데이터를 얼마나 잘 표현하는가를 측정할 때 사용할 수 있는 측도가 가능도함수(우도, Likelihood) 이다.
• 따라서, 모델 파라미터 추정 문제에서 데이터 \(x\)는 이미 알고 있는 값이지만, \(\theta\)는 모르는 값이다.이때는 \(x\)를 이미 알고있는 상수로 놓고 \(\theta\)를 변수로 생각하여 추정하게 된다.
• 이렇게 확률밀도함수에서 파라미터를 변수로 보는 경우에 이 함수는 가능도함수라고 한다.

\[L(\theta;x) = p(x;\theta)\]

• 위의 식에서 L과 p는 관점의 차이이다. L은 \(\theta\) 를 변수로 두고 있는 우도를 구한다는 것이고, p는 \(\theta\) 가 주어졌다고 생각하는 것이지만 우도를 구할때는 파라미터가 추측하는 여러 값으로 변할 것이고 데이터는 이미 관측된 고정값이므로 한 파라미터를 추정할 때 두 식은 같다라고 볼 수 있다.

---

2. 최대 가능도 추정(Maximum Likelihood Estimation, MLE)은 왜 할까?

관찰한 데이터를 가장 잘 설명하는 모델의 파라미터를 찾기 위해서

• 위에서 말했듯 현재 내가 가지고 있는 데이터의 모집단을 가장 잘 설명해줄 수 있는 모델을 찾아야 할때 사용할 수 있다.
• 기계학습에서 유한한 개수의 데이터를 관찰해서 모집단을 정확하게 추정하는 것은 불가능하다. 따라서 모집단을 추정 하게 되는 것이다.
• 여러 모델 파라미터 추정 방법 중 하나가 최대 가능도 추정(Maximum Likelihood Estimation, MLE)이다.
• 최대가능도는 관찰된 데이터 X에 대한 모델 파라미터 \(\theta\) 들이 얼마나 가능한가? 를 계산한다.
• 이때, 각 데이터 X는 독립추출(i.i.d)가정을 하여 각각 \(x_i\) 에 대해 모델 파라미터를 계산할 수 있게 된다.
• 그리고 만들어진 가능도(우도)를 가장 최대로 하기 위한 각 모델 파라미터를 구하기 위해 미분을 사용한다.

---

3. 미분이 불가능한 가능도함수의 경우

• 이때, 미분이 불가능한 모델을 선택한다면 최대값 추정이 아닌 다른 방법을 사용해야 할 수도 있다. 최대 가능도 추정에서는 미분이 가능한 모델을 사용한다고 가정하고 시작한다.
• 그래도 미분이 불가능한 모델을 선택해야한다면 다른 추정법을 고려하거나 미분이 가능하도록 만들 수 있다. 아래와 같은 대안들을 고려하면 된다.

(1) 수치적 최적화 : 우도함수 최적화를 위해 수치적 최적화 알고리즘을 사용(ex. 경사하강법 또는 유전알고리즘)

(2) 단순화된 모델 선택 : 미분이 어려운 모델 대신 미분이 가능한 간단한 모델로 대체하여 추정한다. 이때, 데이터들을 자세히 표현할 수 없는 모델이 선택될 수 있으니 주의해야 한다. 반대의 경우도 있을 수 있다. (over-fitting or under-fitting 문제)

(3) 모델 수정 : 원래 모델을 수정하여 미분이 가능하도록 만든다. 이는 모델의 형태를 변경하거나 특수한 경우에 적용 가능한 변환을 고려해 본다.

(4) 대체 추정 방법 사용 : 모멘트 방법, 베이즈 추정, EM알고리즘 등 다른 추정 방법 사용을 고려한다.

---

4. 최대 가능도 추정에 왜 로그를 사용할까?

• 데이터 숫자 단위를 줄여준다.
• 가능도 함수는 0 ~ 1 사이 범위의 값을 가지는 확률을 독립추출 가정에 의해 모두 곱하기 때문에 값이 너무 작아진다.
• 이는 컴퓨터로 다룰 수 있는 부동소수점의 범위를 쉽게 넘길 수 있으므로 로그를 사용하여 계산 단위를 올려준다.
• 또한, 곱셈이 덧셈으로 치환되어 셈에 용이하다.

---

5. 정규분포를 따르는 가능도함수의 최대 가능도 추정 수식 전개

• 확률변수 : \(X (x_n, x_{n-1}, ... , x_1)\)
• 모델은 정규분포 로 가정한다. 그러면 파라미터로 평균인 \(\mu\) 와 표준편차인 \(\sigma\) 를 갖게된다.
• 모델 파라미터(모수) : \(\theta = (\mu, \sigma^2)\)
• 이를 \(x\) 에 대한 정규분포로 바꿔주면 아래와 같다.

\[f_{X_i}(x_i;\theta) = \frac{1}{\sigma\sqrt{2\pi}} \exp\left(-\frac{(x_i-\mu)^2}{2\sigma^2}\right) , \,\,i=1, \cdots, n\]

• 이제 독립추출을 가정으로한 전체 데이터에 대한 가능도함수(likelihood)를 표현하면 아래와 같다.

\[P(x|\theta) = \prod_{i=1}^{n}f_{X_i}(x_i;\theta)= \prod_{i=1}^{n}\frac{1}{\sigma\sqrt{2\pi}} \exp \left( -\frac{(x_i-\mu)^2}{2\sigma^2} \right)\]

• 양변에 자연로그를 취해 전체를 풀어준다.

\[L(\theta|x) = \ln P(x|\theta) = \sum_{i=1}^{n}\log\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(x_i-\mu)^2}{2\sigma^2}\right)\] \[L(\theta|x) = \ln P(x|\theta)\] \[= \sum_{i=1}^n (\ln \frac{1}{\sqrt{2\pi\sigma^2}} - \frac{(x_i - \mu)^2}{2\sigma^2})\] \[= -\frac{n}{2}\ln(2\pi\sigma^2) - \sum_{i=1}^n\frac{(x_i - \mu)^2}{2\sigma^2}\]

• 전개된 식에서 각 모델 파라미터에 대한 편미분을 하여 최대값을 추정한다. 먼저 평균에 대한 미분이다.

\[\frac{\partial L(\theta|x)}{\partial \mu} = -\frac{1}{2\sigma^2}\sum_{i=1}^{n}\frac{\partial}{\partial \mu}\left(x_i^2-2x_i\mu+\mu^2\right)\] \[= -\frac{1}{2\sigma^2}\sum_{i=1}^{n}(-2x_i + 2\mu)\] \[= \frac{ - n\mu}{\sigma^2} + \frac{\sum_{i=1}^{n}x_i}{\sigma^2}\] \[= \frac{ - n\mu}{\sigma^2} + \frac{\sum_{i=1}^{n}x_i}{\sigma^2} = 0\] \[= - n\mu + \sum_{i=1}^nx_i= 0\] \[\therefore \hat{\mu} = \frac{\sum_{i=1}^n x_i}{n}\]

• 다음으로 표준편차에 대한 미분이다.

\[\frac{\partial L(\theta|x)}{\partial \sigma} = \frac{\partial}{\partial \sigma} [-\frac{n}{2}ln(2\pi\sigma^2) - \sum_{i=1}^n\frac{(x_i - \mu)^2}{2\sigma^2}] = 0\] \[= - \frac{n}{\sigma} + \frac{\partial}{\partial\sigma}[\frac{1}{2\sigma^2} (\sum_{i=1}^n x_i - \mu)^2]\] \[= - \frac{n}{\sigma} - \frac{1}{\sigma^3} (\sum_{i=1}^n x_i - \mu)^2\] \[= - n\sigma^2 - (\sum_{i=1}^n x_i - n\mu)\] \[\therefore \hat{\sigma}^2 = \frac{1}{n}(\sum_{i=1}^n x_i - \mu)^2 = \frac{(n-1)s^2}{n}\] \[(\because s^2 = \frac{1}{n-1} (\sum_{i=1}^n x_i - \mu)^2 )\]

---

6. 코드를 이용한 최대 가능도 추정

• 정규분포에서 평균에 대한 가능도 함수를 그리는 주요 코드를 살펴보면 다음과 같다.

def likelihood_mu(mu):
    return sp.stats.norm(loc=mu).pdf(0)

• 위 함수는 추정치 mu를 입력으로 받아 mu에 대한 가능도를 계산한다.

mus = np.linspace(-5, 5, 1000)
likelihood_mu = [likelihood_mu(m) for m in mus]

plt.plot(mus, likelihood_mu)
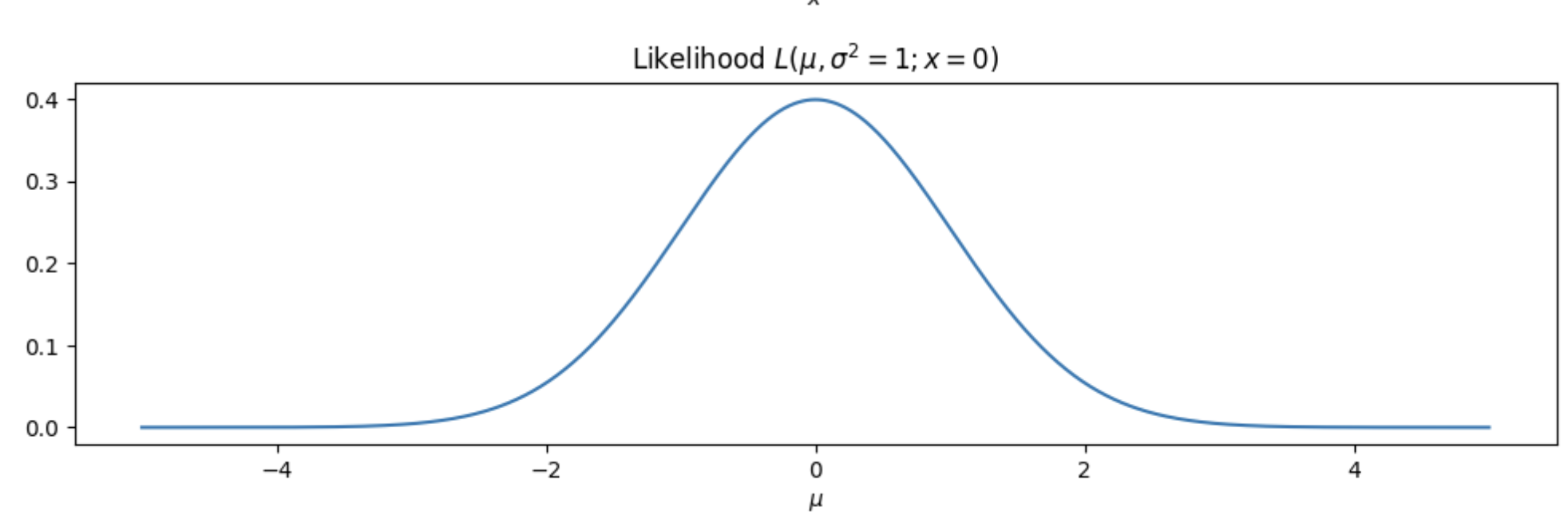
plt.title("Likelihood $L(\mu, \sigma^2=1; x=0)$")
plt.xlabel("$\mu$")
plt.show()

• 위의 결과가 정규분포와 비슷한 모양을 갖는 이유는 주어진 데이터가 정규분포를 따른 다는 가정때문이다.
• 코드에서 사용되고 있는 가능도 함수는 기본값으로 \(\sigma = 1\) 을 가지고, 관측 데이터 \(x = 0\) 에서 정규분포의 확률밀도함수(PDF) 이므로 4가지 이유로 이런 모양이 나타난다.

(1) 정규분포 가정

• 가능도 함수는 관측된 데이터가 정규분포를 따른다는 가정에서 나온다. 정규분포의 확률밀도함수는 특징적인 종 모양 곡선을 가진다.
  

(2) PDF의 곱

• 가능도 함수는 일반적으로 각 데이터 포인트에 대한 확률밀도함수 값들의 곱으로 나타낸다. 다르게 말하면 여러 관측 데이터들에 대한 가능도 함수는 각 데이터를 대입한 각각의 가능도 함수를 곱하여 전체 데이터를 만족하는 가능도 함수를 구한다. 따라서 이 예제에서는 \(x = 0\) 인 하나의 데이터 포인트만 고려하므로 가능도 함수는 각 \(\mu\) 값에서 \(x = 0\) 인 정규분포 확률밀도 함수가 나온다.
  

(3) 정규분포에서 \(\mu\) 변화

• 정규분포에서 \(\mu\) 값을 변화시키면 본질적으로 분포가 x-축을 따라 이동한다. 이 이동은 다양한 지점에서 확률밀도함수 값을 변화시켜, 결과적으로 가능도 함수도 이에 따라 변화한다.
  

(4) 종 모양 곡선

• 정규분포가 종 모양 곡선을 가지는 특성으로 인해 \(\mu\) 에 대한 가능도 함수도 비슷한 모양을 갖게 된다. \(\mu\) 가 관측된 데이터 지점에서 멀어질수록 가능도는 감소하고, 이에 다른 평균 값에서 주어진 데이터 지점을 관측할 확률이 감소함을 나타낸다. 쉽게 말하면, 관측된 데이터 지점이 하나 뿐이므로 당연히 \(\mu\) 도 그 값을 기준으로 밖에 생길 수 없기 때문에 예제에서 이런 모양이 나타난다.
  

결국, \(\mu\) 에 대한 가능도 함수가 정규분포와 유사한 모양을 갖는 것은 가능도 함수 자체가 주어진 데이터 지점을 다양한 평균 값에서 관측할 확률을 나타내기 때문이다. 이것이 정규분포의 파라미터를 추정할 때 최대가능도추정을 사용하는 경우의 기본적인 특성이다.

• 표준편차도 동일한 과정으로 구할 수 있다.

---

7. 베르누이 분포(Bernoulli Distribution)에 대한 최대 가능도 추정

• 위에서는 정규분포에 대한 최대 가능도 추정 식 전개와 코드를 살펴보았다.
• 모델은 어떤 것이든 사용될 수 있으므로, 이번엔 이산분포의 기본인 베르누이 분포를 이용한 최대 가능도 추정을 전개해 보겠다.